Fractal Worlds
A fractal is a curve or geometrical figure, each part of which has the same statistical character as the whole
I was always fascinated by complex structures emerging over simple rules. In school I stumbled over the Youtube channel Numberphile, which presented some really interesting math concepts, including fractals which fascinated me right away. It is as visualizing the fractal patterns behind simple formulas reveals already existing worlds, embedded and hidden in the maths, waiting to be discovered, sometimes looking shockingly close to known structures…
But what is a Fractal?
My simplest intuitive definition is that it is a recursive pattern, so it has infinite intricacy while zooming in, revealing its repetitive patterns. Because it is defined recursively, its complexity is perfectly compressible into (simple) rules.
One of the most prominent and fascinating instances is the Mandelbrot Fractal and its related fractals, such as Julia sets, Multibrot sets, the Burning Ship fractal and my favorite: the Bhuddabrot and its RGB version the Nebulabrot. And no, it has nothing to do with the german word mandel (almond) or brot (bread), it is named after its discoverer, the mathematician Benoit Mandelbrot.
Hmm… Almondbread
The Mandelbrot set is simply defined as the set of complex numbers \(c\in \mathbb{C}\) for which the sequence
\[z_{n+1}=z_n^2 + c\]starting at \(z_0 = 0\) is bounded. For visualization we simply graph each \(c\) as a 2D point (real part on x-axis, imaginary part on y). The points of the Mandelbrot set are simply colored black. However the magic happens when plotting the divergence of the sequence at the borders of the set. Given a color scale, we simply relate the speed of divergence for each \(c\) to a color. Thats it…
Zooming into the mandelbrot fractal
It is fascinating how this simple formula reproduces such intricate new worlds when plotted in such a way. Makes one think if our own universe is a fractal (stay tuned).
Although infinitely repeating, there are many iconic substructures in the Mandelbrot fractal, such as the elephant valley or the seahorse valley, located in the region between the left and right big bulb:
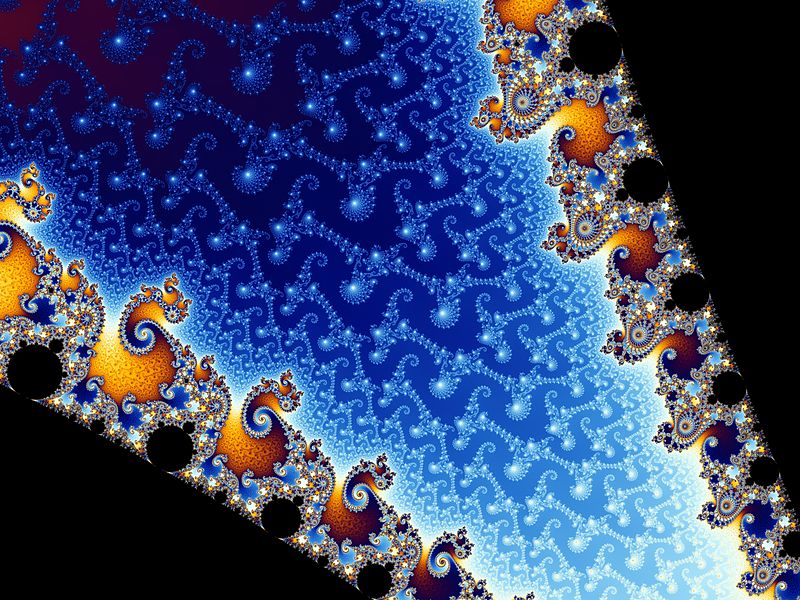seahorse valley, one of the iconic substructures in the Mandelbrot fractal
So far we only mapped the different \(c\) values of the sequence to the pixels. If we instead keep \(c\) constant and map the \(z_0\) values to each pixel, we obtain the related Julia fractals and sets for each point in the mandelbrot fractal, which themselves are subpatterns in the mandelbrot fractal.
There are many more hidden connections in the mandelbrot set, such as \(\pi\) hiding in scaling properties of its self-similar structures and external angles in the complex plane, but this would be far to technical for this post (for the interested: Pi in the mandelbrot set).
Butterbrot, oh sorry Bhuddabrot
The Bhuddabrot is also closely related to the Mandelbrot fractal: As before each pixel represents a range of complex values, but instead of coloring by the grade of divergence, we count how often each pixel is visited for diverging sequences when computing up to \(z_{max}\) with \({max} \in \mathbb{N}\) and gray values according to the number of visits.
The higher we set \(max\) and the resolution the more details come into view. Rotated by 90 degrees, the result is a meditating Bhudda with precious headdress:
Bhuddabrot with 20000 iterations
For a more colorful image we can also assign each color channel (e.g. RGB) a different \(max\) and then count separated for each channel by its \(max\), which results in the beautiful Nebulabrot:
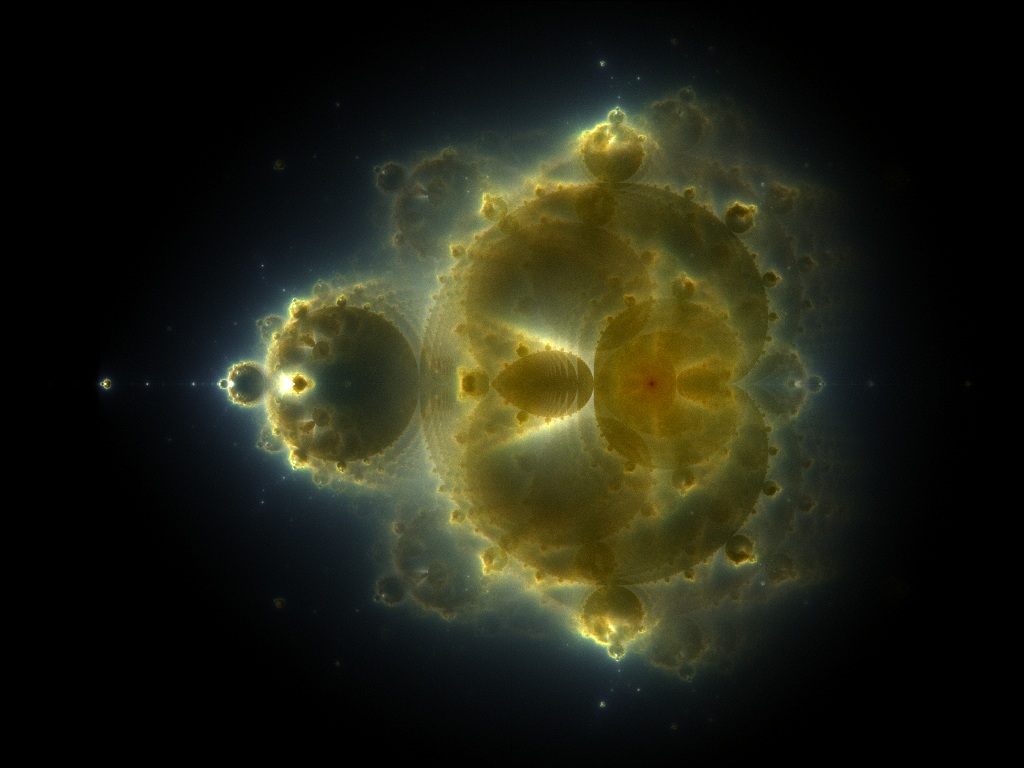Nebulabrot with \(max_r = 2000, max_g = 200, max_b = 20\)
There is a direct relation to the Mandelbrot allowing for rotation choosing the right projections, from the Bhuddabrot to the Mandelbrot and back:
Rotating between Mandelbrot and Bhuddabrot
Credits to Benedikt Bitterli, check out his work here to learn how he built this beautiful animation.
Its getting weirder…
Exploring fractals goes beyond the Mandelbrot set and its beautiful derivatives. There are some related fractals which I will include here as honorable mentions. Such as the asymmetric Burning Ship and higher-dimensional versions of the Mandelbrot.
Burning Ship Fractal
| Zoomed Out | Zoomed into right antenna |
|---|---|
 |  |
Asymmetric fractal with intricate ship and cathedral-shaped patterns constructed similarly to the Mandelbrot, by using a modified formula. (Images: Softology’s Blog)
The series for computing the Burning Ship fractal (Plotted the same as for the default Mandelbrot) is defined as:
\[z_{n+1} = (|\operatorname{Re}(z_n) | + i |\operatorname{Im}(z_n)|)^2 + c, \quad z_0 = 0\]where the functions \(\operatorname{Re}\) and \(\operatorname{Im}\) return the real and imaginary parts of the complex number, respectively.
Higher Dimensions: Almonds, Bulbs and Boxes
For 3D and 4D there exist two visually pleasing Mandelbrot descendants, the Mandelbulb and the 4D Mandelbrot:
The Mandelbulb is constructed as the 3D equivalent of the Mandelbrot set. Since 3D complex numbers do not exist, we use vectors in \(\mathbb{R}^3\). The Mandelbulb formula extends the power and magnitude calculations into three dimensions using spherical coordinates.
The 4D version of the Mandelbrot is constructed using Quaternions, which are the 4D equivalent to complex numbers \(\mathbb{C}\). Visualizing this fractal in a comprehensible manner is hard, but by binding one dimension to time, we can iterate through the 3D slices of the 4D fractal, producing mesmerizing morphing structures.
Mandelbulb (3D)
Mandelbrot (3D projection of 4D Mandelbrot)
Mandelbrot (4D)
Fractals in Nature
Fractals are everywhere — in snowflakes, shells, trees, vegetables (such as Romanesco), and more. In a follow-up article, we will explore the connection and use of fractals in nature and if the universe could be a fractal itself:
Recursive blueprints, expressed in fractals, enable the formation of stable, intricate structures emerging from self-organizing systems, ranging from crystals to complex life forms. Their advantageous properties, such as high compressibility for efficient storage in the genomes of organisms and ease of construction in multi-agent systems (where each cell acts as an agent), make them an evolutionary solution in diverse problem spaces.
Stay tuned :)